What is a Coordinate Frame?
Conceptually, a coordinate frame describes the world from the perspective of an observer inside the world. It consists of a position in the world (the coordinate frame's origin), and a coordinate system (the X, Y, and Z directions from the point of view of the observer).
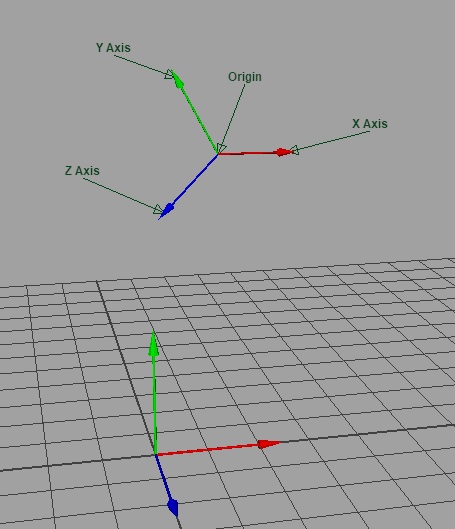
Components of a Coordinate Frame
The three vectors used to specify the X, Y, and Z directions need to be unit length and orthogonal. If they are not, then objects will appear skewed and scaled from the point of view of coordinate frame.
Coordinate Frame Example
The figure shows three coordinate frames. The standard world coordinate frame is always at the origin with the unit vectors in standard X, Y, and Z directions. It always necessary to have an absolute reference frame from which to describe other coordinate frames.

Coordinates of Sphere
I am using homogeneous coordinates to define points and vectors. Points have a W component of 1 and vectors have a W component of 0. This is an important distinction later when doing matrix-vector multiplication. Points are capable of translation and rotation in space. Vectors, on the other hand, can only be rotated. Vectors are defined by a magnitude and direction and have no concept of position. Using homogeneous coordinates will allow us to take advantage of this distinction with a single matrix operation.
\( \begin{align*} P &= [x, y, z, w=1] \\ \vec{V} &= [x, y, z, w=0] \end{align*} \)
World Frame
Coordinate System Vectors
\( \begin{align*} \vec{X}_{W} &= \begin{bmatrix} 1 & 0 & 0 & 0 \end{bmatrix} \\ \vec{Y}_{W} &= \begin{bmatrix} 0 & 1 & 0 & 0 \end{bmatrix} \\ \vec{Z}_{W} &= \begin{bmatrix} 0 & 0 & 1 & 0 \end{bmatrix} \\ \end{align*} \)
Coordinate Frame Origin
\( \begin{align*} O_{W} &= \begin{bmatrix} 0 & 0 & 0 & 1 \end{bmatrix} \\ \end{align*} \)
Coordinates of the Sphere
\( \begin{align*} P_{W} &= \begin{bmatrix} 2 & 2 & 0 & 1 \end{bmatrix} \\ \end{align*} \)
Frame 1
Coordinate System Vectors
\( \begin{align*} \vec{X}_{F1} &= \begin{bmatrix} \phantom{-}0 & -1 & \phantom{-}0 & \phantom{-}0 \end{bmatrix} \\ \vec{Y}_{F1} &= \begin{bmatrix} \phantom{-}1 & \phantom{-}0 & \phantom{-}0 & \phantom{-}0 \end{bmatrix} \\ \vec{Z}_{F1} &= \begin{bmatrix} \phantom{-}0 & \phantom{-}0 & -1 & \phantom{-}0 \end{bmatrix} \\ \end{align*} \)
Coordinate Frame Origin
\( \begin{align*} O_{F1} &= \begin{bmatrix} -2 & 2 & 0 & 1 \end{bmatrix} \\ \end{align*} \)
Coordinates of the Sphere
\( \begin{align*} P_{F1} &= \begin{bmatrix} 0 & 4 & 0 & 1 \end{bmatrix} \\ \end{align*} \)
Frame 2
Coordinate System Vectors
\( \begin{align*} \vec{X}_{F2} &= \begin{bmatrix} -1 & \phantom{-} 0 & \phantom{-} 0 & \phantom{-}0 \end{bmatrix} \\ \vec{Y}_{F2} &= \begin{bmatrix} \phantom{-} 0 & -1 & \phantom{-} 0 & \phantom{-}0 \end{bmatrix} \\ \vec{Z}_{F2}&= \begin{bmatrix} \phantom{-} 0 & \phantom{-} 0 & \phantom{-} 1 & \phantom{-}0 \end{bmatrix} \\ \end{align*} \)
Coordinate Frame Origin
\( \begin{align*} O_{F2} &= \begin{bmatrix} 3 & 3 & 0 & 1 \end{bmatrix} \\ \end{align*} \)
Coordinates of the Sphere
\( \begin{align*} P_{F2} &= \begin{bmatrix} 1 & 1 & 0 & 1 \end{bmatrix} \\ \end{align*} \)
As you might have expected, there are three different coordinates for the position of the sphere depending on which coordinate frame you are referencing. All of these coordinates are equally valid coordinates for the sphere (there isn't a set of coordinates which are more "correct" than another). However, it's now clear that when you refer to the coordinates of the sphere, you are always referring to its coordinates in terms of a specific coordinate frame. If not explicitly stated, it is implied that the coordinates are set in the standard world coordinate frame.